
The generation and diffusion of scientific knowledge and technology are assumed to be drivers of modern economic growth, but there is a lack of firm empirical evidence of this. This column uses the first detailed data on the density of engineers in the western hemisphere to argue that historical differences in innovative capacity, as captured by the density of engineers in 1880, explain a significant fraction of the Great Divergence. The results confirm the imperative of developing higher-order human capital.
The generation and diffusion of scientific knowledge and technology are fundamental drivers of modern economic growth. Authors agree that human capital is an important part of the innovative capacity required to facilitate this process, but it is not clear which type of human capital is most important. Some have argued for literacy, secondary, or tertiary education, while others stress higher-order technical skills (Goldin and Katz 2009). In his classic article on endogenous growth, Romer (1990) puts the research engineer at centre stage. From a historical perspective, Mokyr (2005) decides that scientifically minded and engineering-minded technicians were instrumental in industrialisation. These so-called 'upper tails of knowledge' are thought to have been particularly important during the second Industrial Revolution between 1870 and 1914.
The lack of systematic historical data on either the prevalence or impact of engineers on income has made it hard to confirm empirically the importance of these skills. Conceptually, Murphy et al. (1991) argue for the importance for modern growth of engineering, compared to less productive professionals such as lawyers. More recently, Cantoni and Yutchman (2014) show higher growth closer to medieval universities, and Squicciarini and Voigtländer (2015) relate faster French industrialisation in 1750 to Encyclopedie subscriptions. To date, however, neither the historical prevalence of Romer's research engineers nor Mokyr's engineers and mechanics have been quantified in a globally comparable form. In our recent work (Maloney and Valencia Caicedo 2017), we argue that historical differences in innovative capacity, as captured by the density of engineers in 1880, explain a significant fraction of the Great Divergence in the Western Hemisphere as documented by Galor (2011), among others.
Density of engineers in 1900
Our initial contribution to the debate has been through data collection. We have created the first systematic information on the density of engineers at the country level – and additionally for the US and Americas at the state or county level – for the western hemisphere. Geolocated patenting density data for the US allow us to tease out innovative versus adoptive capacity (as posited by Mokyr 1992). We control for other levels of education that, as mentioned before, may also have been important, including basic literacy, secondary schooling, college attendance, and the presence of other high-level professions such as lawyers and physicians.
Figure 1 shows number of engineers per 100,000 workers in 1900. This period is critical since it captures the second Industrial Revolution, in which science and invention became more institutionalised, meaning that specific high-end human capital skills become critical to inventing or transferring technologies. This was generated by aggregating graduates from local engineering programmes, augmented with information from censuses and professional societies. It is immediately clear that countries that had very similar levels of income had widely different engineering density. Chile, Argentina, Denmark, Sweden, and the American South are all at similar levels of income in 1900, yet the Nordic countries have densities of 100, the American South (a relatively backward region at the time) 60, and Chile, Argentina, and the rest of Latin American, less than 20. The colonial mother countries of Spain and Portugal also had low density of engineers. At the other end of the spectrum is Sweden, the impoverished sophisticate, because it was too poor to employ all the people it educated. It is striking that these engineering differentials predict the subsequent divergence in incomes: Sweden’s and Denmark’s surge, and Argentina’s stagnation.
Figure 1 National engineering density: Americas and selected European countries
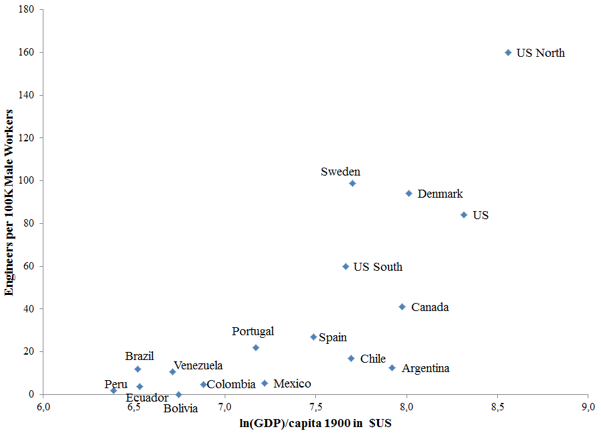
Source: Plot of GDP per capita in 1900 from Maddison.
Note: Engineering density is accumulated graduates of engineering programs per 100,000 male workers around 1900.
Main findings
To empirically ground the relationship more carefully, we employ data on engineers and patenting activity at the county level for the US in 1880 (the earliest available year) and for six countries in the Americas at state level. This data are robustly correlated with current income after controlling for a wide variety of economic, social and educational variables. The quantitative effects are also important: a one standard deviation increase in engineers in 1880 accounts for a 16% increase in US county income today, and patenting capacity contributes another 10%. Patenting appears to capture a different kind of innovative human capital from engineering. Perhaps patenting captures more inventive activity, and engineering more adoptive capacity. We also find lawyers were complementary to engineers at this point, perhaps due to their role in setting up institutional rules, or their role in registering patents.
Figure 2 State engineering density in US and Mexico, circa 1900
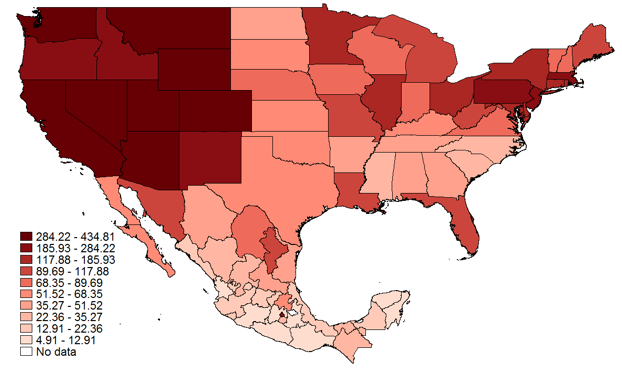
Source: Engineering density at the subnational level for North America.
Note: Derived from census reported engineers per 100,000 male workers around 1900.
To tackle the potential endogeneity of engineering training, we use the distance to the closest Morrill Land Grant College. This is likely to be a good instrument because the establishment of the Land Grant colleges (1862 and 1890) was largely supply-driven and uncorrelated with demand for engineering services arising potentially from other drivers of growth. We show that the 1862 programme led to more engineering graduates in 1880, which was not the case for lawyers or physicians. We also use the 1890 wave as a placebo, showing that it had no effect on our earlier engineering measure. In less detail, due to data availability, we show that more engineers were also associated with higher levels of income at the state level for a panel of countries in the Americas (for a stark illustration of this, see Figure 2). Applying the well-estimated coefficients of the county-level regressions to the different countries in the sample, we are able to explain up to one-third of the variance of income across the Western Hemisphere.
In general, our results inform the discussion about the importance of the upper tails of the educational distribution in growth. The US, as in Europe, had a very well-articulated engineering establishment by 1900 – specialised engineering departments in chemical, civil or mechanical engineering – as well as differentiated professional societies. The secondary school movement didn’t begin until after 1910 and, at this moment, approximately 7% of the population had a secondary education. Hence, for developing countries a case can be made both for investing in basic education as well as higher-order technical education.
Mechanisms and drivers
We examined the possible mechanisms behind the effects on long-run income by looking at intermediate historical outcomes. Engineering density appears positively correlated with technological adoption and structural transformation 50 years after our engineering measure. The sophistication of manufactures, the share of manufactures, and the development of entrepreneurship proxied by retail and wholesale establishments, are all highly correlated with engineering density, again consistent with Murphy et al. (1991). We observe a hump-shaped relationship for manufacturing value added peaking around 1920 (Figure 3). We hypothesise that it was precisely the enhancing of structural transformation which led to growth in the long term. We do not observe, in turn, a significant effect in more agricultural areas. Case studies from the US and Latin America, centred on mining, confirm our empirical results and the mechanisms at play.
Figure 3 Engineering density as a determinant of manufacturing value, 1860-1940
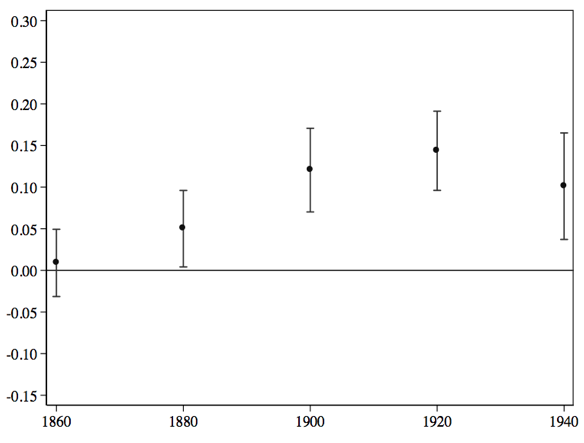
Notes: The figure plots the coefficient of engineering density on manufacturing value added at 20 year intervals from 1860 to 1940. Beta coefficients. Lines mark 95% confidence intervals.
Lastly, we explored the possible drivers of innovative capacity. We found that, in the US, slavery appears to have been a major deterrent to the development of engineering capacity and this could be one of the principal channels through which slavery slowed the growth of the South. Population density, on the other hand, appears significantly positive. We further hypothesise that key cultural factors such as colonial heritage, migration and religion might have determined innovative capacity (as in Benabou et al. 2015). The similarly low levels of engineering density across Latin America, and the mother colonial countries of Spain and Portugal, suggest that the New World inherited many institutions and cultural traits from Spain’s and Portugal's weak innovative capacity.
Conclusions
Our measures of higher-order technical human capital and their impact on income offer empirical support for endogenous growth theory. They also complement the historical evidence around the importance of upper tail knowledge for the second Industrial Revolution. This is most clearly documented for the US at the county level. More broadly, the tenfold differences in engineering density plausibly explain how growth in countries with similar levels of income in 1900 diverged in the 20th century. Our results confirmed the imperative of developing higher-order human capital and, more broadly, the national capacity to identify and adopt new technologies from abroad for emerging regions.
References
Benabou, R, D Ticchi and Vindigni (2015), “Religion and innovation”, The American Economic Review, 105(5), 346-351.
Cantoni, D and N Yuchtman (2014), “Medieval universities, legal institutions, and the commercial revolution”, The Quarterly Journal of Economics, 129(2), 823-887.
Galor, O (2011). Unified Growth Theory. Princeton, NJ: Princeton University Press..
Goldin, C and L F Katz (2009). The Race between Education and Technology. Belknap of the Harvard University. Cambridge.
Maloney, W F and F Valencia Caicedo (2017), “Engineers, Innovative Capacity and Development in the Americas.” CESifo Working Paper No. 6339. Munich.
Mokyr, J (1992). The lever of riches: Technological creativity and economic progress. Oxford: Oxford University Press.
Mokyr, J (2005), “The intellectual origins of modern economic growth”, in A Quadrio Curzio and M Fortis (eds), Research and Technological Innovation (pp. 17-80). Physica-Verlag, HD.
Murphy, K M, A Shleifer and R W Vishny (1991), “The allocation of talent: Implications for growth”, The Quarterly Journal of Economics, 106(2).
Romer, P M (1990), “Endogenous technological change”, Journal of Political Economy, 98(5).
Squicciarini, M P and N Voigtländer (2015), “Human capital and industrialization: Evidence from the age of enlightenment”, The Quarterly Journal of Economics, p.qjv025.


