Adaptive experiments for policy research

One of the biggest methodological shifts in public policy research has been the rise of experiments, or randomised controlled trials (RCTs). RCTs have been particularly influential in development economics (Banerjee et al. 2016). 

When academic researchers conduct an RCT, their goal is typically to measure the outcome of interest as precisely as possible. For example, they may want to compare labour market outcomes after completing a job search training module (the treatment) against the status quo without training (the control). This is best done by creating treatment and control groups that are similar in size and composition (see Athey and Imbens 2017). Such RCTs can answer the question, “does this programme have a significant effect?” 

However, when a government or NGO conducts an experiment, their objective is often slightly different. For instance, they may be more interested in quickly choosing between several possible programme variants. In other words, they would like to answer, “which programme will have the greatest effect”? 

Building flexibility into experimentation

Precision Agriculture for Development (PAD) provides a free agricultural extension service for smallholder farmers. Farmers only have to answer a few questions over the phone to be enrolled. For an enrolment drive in India with 1 million farmers, PAD did not need to estimate enrolment rates precisely; rather, they wanted to learn as quickly as possible how to conduct enrolment calls so farmers wouldn’t screen them out before even learning about the service. 

The idea behind ‘adaptive experimentation’ is that we should tailor the experimental design to the exact learning objective of the experiment. In particular, if the experiment can be conducted in several waves, we learn and adapt the design at each wave. For PAD, the objective was to identify the enrolment method with the highest success rate for use after the experiment; in other cases, it might be to assign treatments that generate the best possible outcomes for the participants during the experiment. But even when the goal is treatment effect estimation, as in a ‘classical’ RCT, adaptivity can improve learning (see Hahn et al., 2011).  

In the first wave, an adaptive experiment may look just like a non-adaptive RCT. However, this changes as we learn how the different options perform. For example, when the objective is to identify the best option out of many, assignment should focus on higher-performing options as the experiment progresses in order to learn as much as possible about those choices that are likely candidates for implementation. 

Prioritising treatments that show effectiveness 

The idea of adaptive sampling is almost as old as the idea of randomised experiments; see, for instance, Thompson’s early proposal in 1933. Adaptive designs have been used in clinical trials (Berry 2006, FDA 2018), and in the targeting of online advertisements (Russo et al. 2018). Thompson, like many after him, discusses the second objective above, namely that participants during the experiment have the highest possible outcomes. This is playfully termed a ‘multi-armed bandit problem’, after a gambler who needs to decide which ‘one-armed bandit’ to feed with coins for the highest chance of winning. The gambler faces the famous exploration-exploitation trade-off: She would learn the most by pulling different bandit arms repeatedly, but after a few tries, some arms have had better payoffs and therefore are much more attractive to continue to pull. 

The gambler’s best approach tends to be to pull more lucrative arms proportionally more often. By analogy, an experimenter should assign the most participants to the treatment arm that was most successful in earlier waves, but still devote a share of the sample to the other arms. This way more participants benefit from the better treatments than in a non-adaptive RCT. Of course, we cannot assign all to the best arm; we are running the experiment to find out which arm that is. 

Adaptive experiments can be designed for many different objectives, or even combine them. For example, in a job search support program for refugees in Jordan by the International Rescue Committee, researchers implemented a hybrid of a multi-arm bandit and a standard RCT to evaluate the effects of providing information sessions, counselling, or financial support. This design achieves better treatment outcomes than a pure RCT while also learning about each treatment arm with high precision (Caria et al. 2020). 

Figure 1 Image of a ‘liberty bell’ slot machine by Charles Fey from 1899, with the ‘arm’ on the right

Source: Nazox (CC BY-SA 3.0).

Finding the right balance between treatments

One obstacle to adaptive experiments is that it is difficult to calculate the exact optimal treatment allocation. Fortunately, however, there are algorithms that can provide good approximations. So-called Thompson sampling is popular for the bandit problem, for example  (see Russo et al. 2018). 

In recent research (Kasy and Sautmann, 2020), we propose a new algorithm for the objective of finding and implementing the best policy option, like PAD wanted to do. We call this algorithm ‘exploration sampling’. It is based on Thompson sampling, but puts stronger emphasis on learning about the best option (exploration). The idea is that it may sometimes be a priority to learn as quickly as possible and implement the best option after the experiment is over. 

This can be justified when ongoing testing is not feasible, perhaps because it is not practical to implement many treatment arms in parallel or collect data for long periods, or because there is political resistance to ‘never-ending experiments’. Another case is when outcomes during the testing phase are simply not relevant; for example, when piloting different interview protocols, the pilot observations cannot be used in the final data analysis. 

Key findings

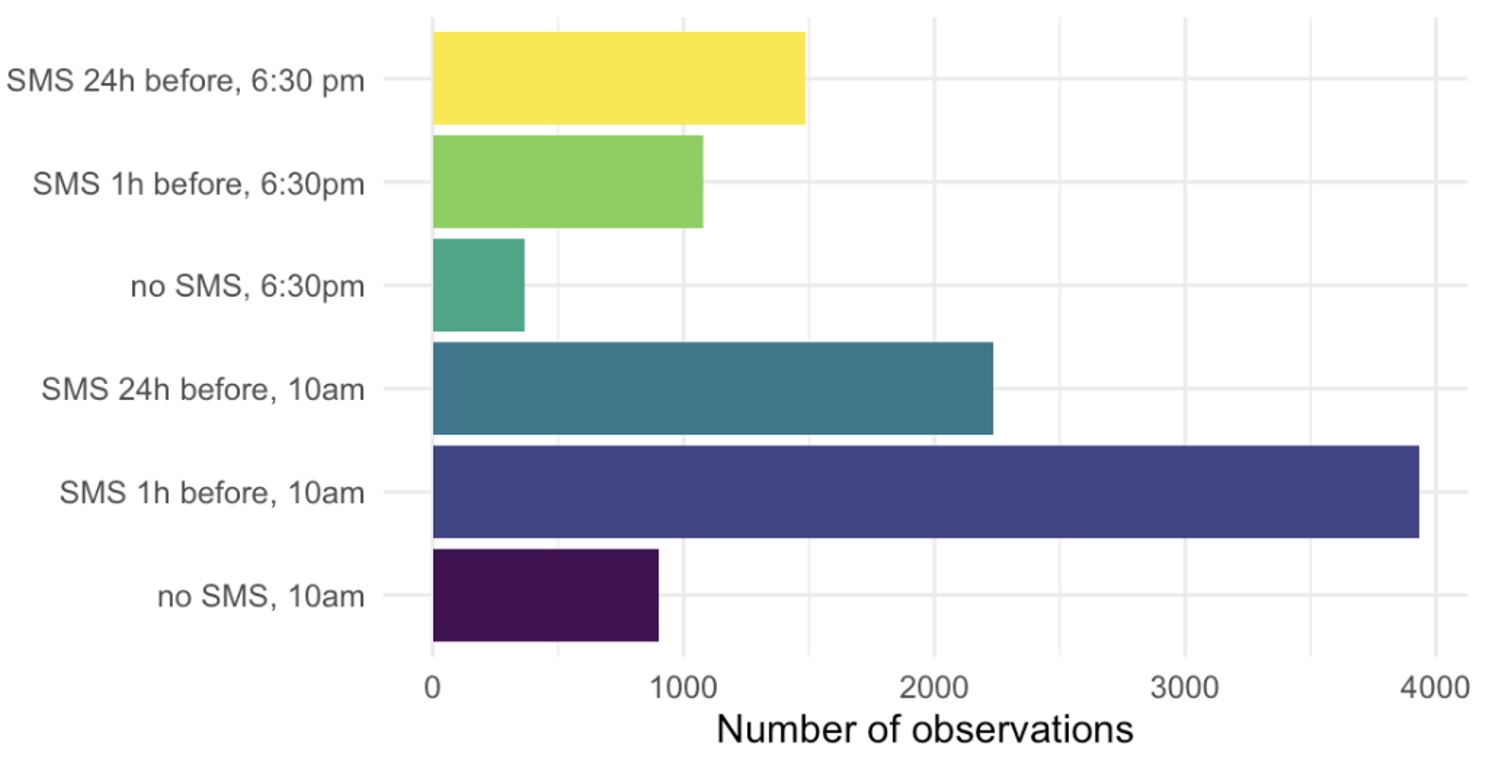
We show that exploration sampling leads to consistently better policy recommendations than a standard RCT or Thompson sampling. In PAD’s case, we implemented exploration sampling with 10,000 phone numbers in June 2019. PAD tested placing calls in the mornings or evenings, and alerting the farmer with a text message at different lead times. Figure 2 shows the share of successful calls in the six treatment arms by the end of the experiment, and Figure 3 illustrates assignment shares over time. Despite considerable variation, calling at 10 am with a text message one hour ahead emerged as the most successful treatment early on. As a result, nearly 4,000 numbers were assigned to this arm (aggregate assignment shares in Figure 4).

Figure 2 Share of successful calls in each treatment arm

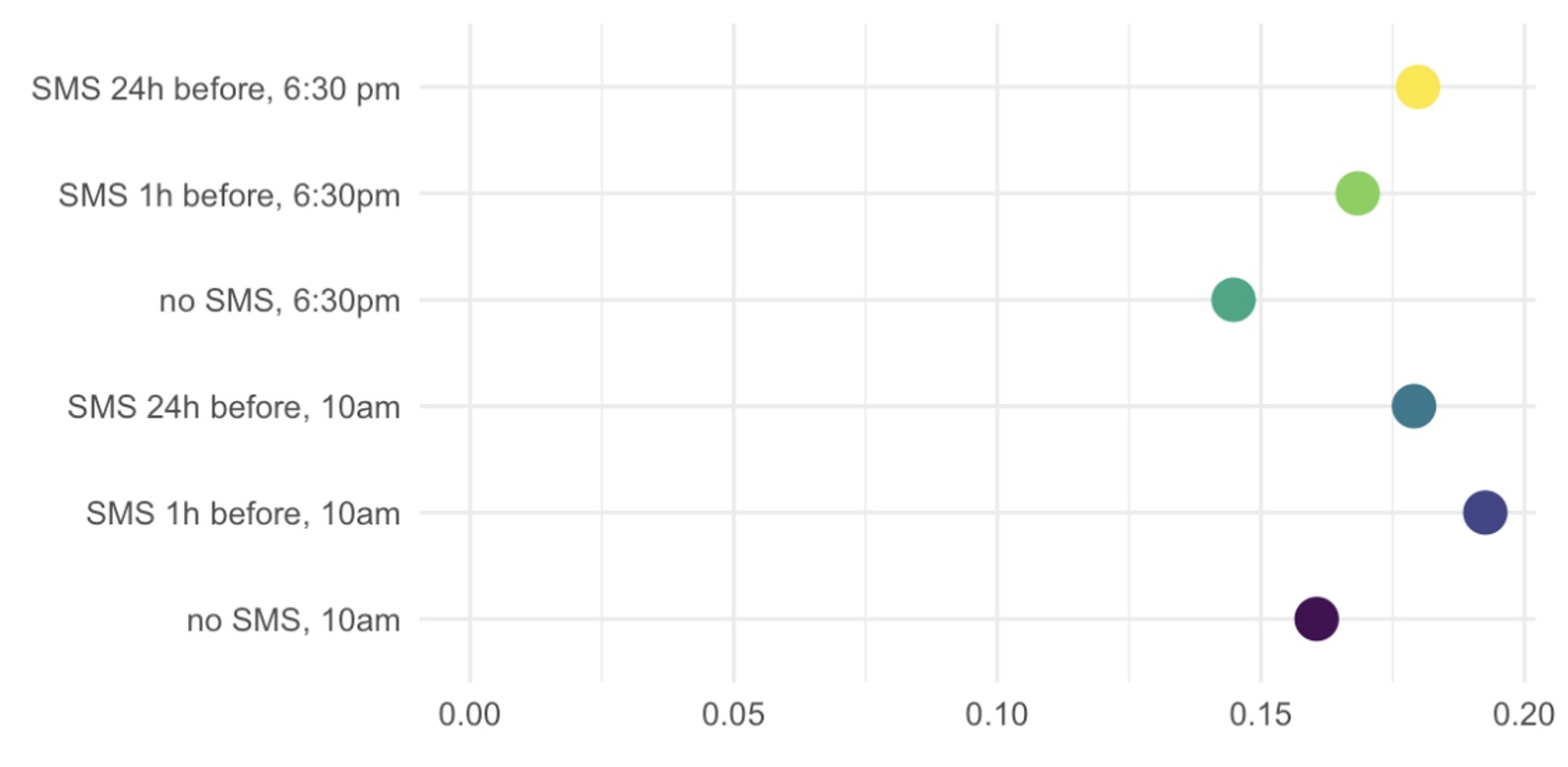
Figure 3 Assignment shares over time

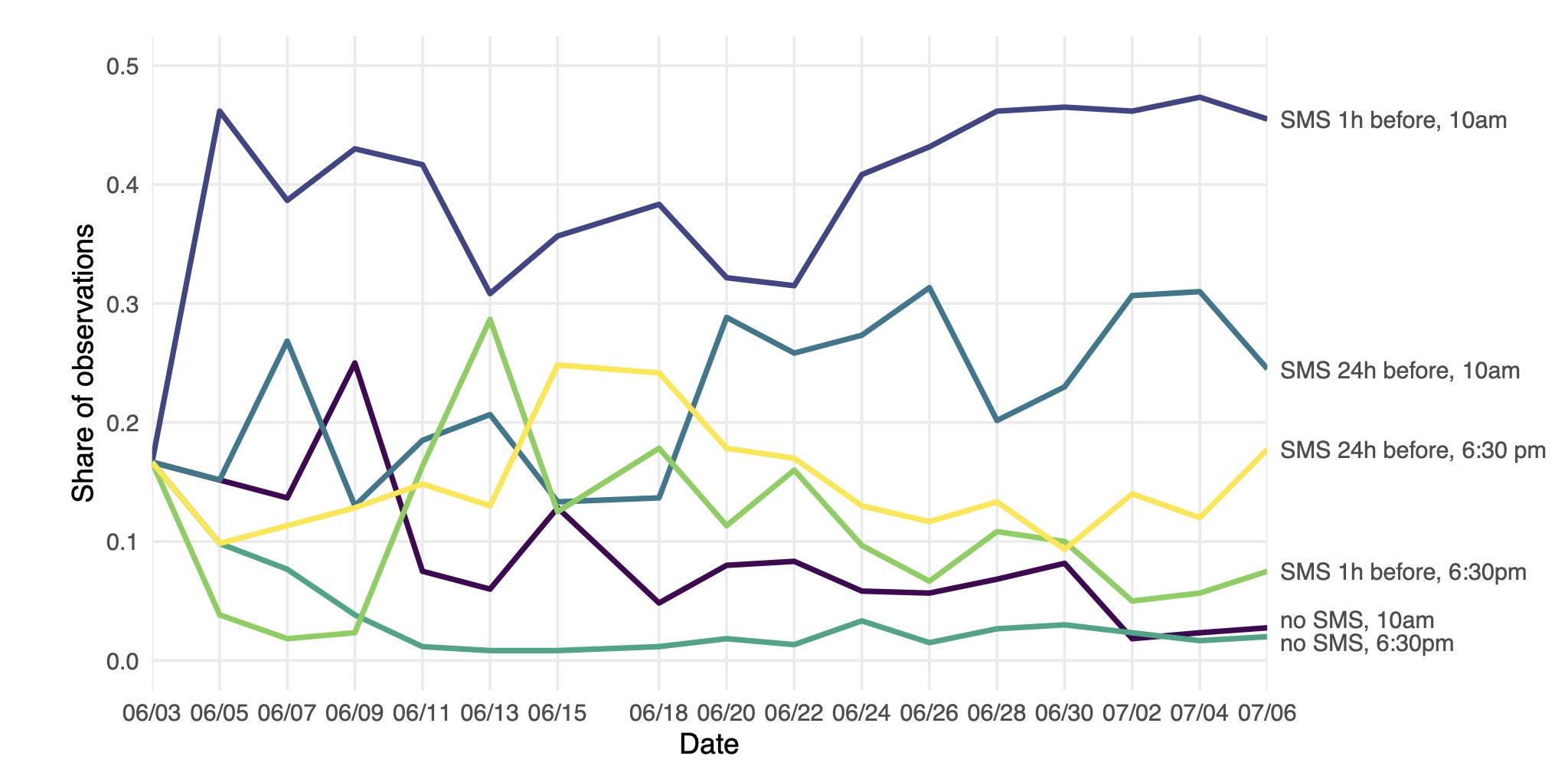
Figure 4 Aggregate number of observations (phone numbers) assigned to each treatment arm at the end of the experiment

Lessons for future experimentation

PAD’s example shows that adaptive sampling has great potential to improve the way we conduct experiments for purposes other than pure treatment effect estimation. Adaptivity provides a systematic way of running pilot studies or ‘tinkering’ with policy options, perhaps in the spirit of what Esther Duflo termed ‘the economist as plumber’ (2017). Algorithms like Thompson sampling or exploration sampling ensure that the learning process and resulting decision are fast, replicable, and empirically justified. As a welcome consequence, more participants benefit from the best treatment options, facilitating the ethical conduct of experiments in development and policy research.

Editors’ note: A version of this article first appeared on GlobalDev. The findings, interpretations, and conclusions expressed in this article are entirely those of the authors. They do not necessarily represent the views of the World Bank and its affiliate organizations, or those of the Executive Directors of the World Bank or the governments they represent.

References

Athey, S and GW Imbens (2017), “The econometrics of randomized experiments”, Handbook of Economic Field Experiments, volume 1, pages 73–140. Elsevier. 

Banerjee, A, E Duflo and M Kremer, (2016), “The influence of randomized controlled trials on development economics research and on development policy”, MIT. 

Berry, D (2006), “Bayesian clinical trials”, Nature Reviews Drug Discovery, 5(1): 27–36.

Caria, S, G Gordon, M Kasy, S Quinn, S Shami and A Teytelboym (2020), “An Adaptive Targeted Field Experiment: Job Search Assistance for Refugees in Jordan”,  CESifo Working Paper Series 8535, CESifo.

Duflo, E (2017), “Richard T. Ely lecture: The economist as plumber”, American Economic Review, 107(5): 1–26. 

FDA (2018), “Adaptive designs for clinical trials of drugs and biologics, guidance for industry”, U.S. Department of Health and Human Services, Food and Drug Administration.

Hahn, J K Hirano and D Karlan (2011), “Adaptive Experimental Design Using the Propensity Score”, Journal of Business & Economic Statistics, 29(1): 96-108.

Kasy, M, A Sautmann (2020) “Adaptive treatment assignment in experiments for policy choice”, Econometrica 89(1): 113-132.

Russo, D (2016), “Simple bayesian algorithms for best arm identification”, Conference on Learning Theory, pages 1417–1418. 

Russo, DJ, BV Roy, A Kazerouni, I Osband and Z Wen (2018), “A Tutorial on Thompson Sampling,” Foundations and Trends® in Machine Learning, 11(1): 1–96. 

Thompson, WR (1933), “On the likelihood that one unknown probability exceeds another in view of the evidence of two samples”, Biometrika, 25(3/4): 285–294.