What are the long-term returns to large-scale education expansions?

Large-scale educational expansions represent substantial investments of public resources and potentially benefit households by increasing education levels and therefore productivity in the local economy. However, since they impact both individual behaviour and labour markets, convincing causal estimates of their overall benefits are hard to generate. While small-scale, carefully controlled, researcher-led experiments provide promising evidence about which educational investments are effective (Muralidharan et al. 2019), for a variety of reasons these estimates may not be valid for large-scale policies. Importantly, large-scale education programmes may have sizable general equilibrium (GE) effects beyond the individual, for example in the education sector and the labour market, that may either undermine or enhance the effectiveness of the intervention (Heckman et al. 1998). Accurately estimating and understanding these GE effects are therefore crucial to assessing the overall benefits of nationwide investments in education.

Students who get more schooling because of such policies may earn higher wages, but they are not affected in isolation. In the labour market, an expansion in schooling makes skilled workers more abundant and lowers their equilibrium earnings (Card and Lemieux 2001). At the same time, an increase in the size of the skilled workforce may attract capital and technology, benefiting skilled workers. These changes to the structure of the local economy will affect benefits to workers by changing the labour market returns to schooling – a parameter that labour economists have been debating for at least the last half century (Mincer 1975). In the education sector, on the other hand, additional public schools may simply crowd-out private schools, diminishing the benefits of schooling expansions. In my research (Khanna 2023), I develop a new framework to causally estimate these GE effects, and determine the overall economic consequences of a nationwide education programme in India.

The framework of my research

For my research, I build a new framework to analyse the consequences of a large-scale educational expansion programme in India with an explicit focus on issues that are inherent to nationwide government policies: most importantly the GE effects in the markets for both education and labour. I model firms, households, private and public schools. I then split up the overall changes in wages into the direct effects of schooling and the indirect effects that occur as a result of surrounding people getting more education. The model guides us to what to estimate, and I use a Regression Discontinuity (RD) approach to estimate these.

The policy I study is the District Primary Education Programme (DPEP), which expanded public schooling in half the country by targeting low-literacy regions. It was the Indian government's flagship scheme in the 1990s and early 2000s, and at that time was the largest programme for primary education in terms of geography, population and funding, suggesting that its effects would be similarly broad. The allocation rule under which districts receive the funding allows me to estimate the parameters of the model using a Regression Discontinuity (RD) approach. The policy rules were such that districts that had a female literacy rate below the national average were more likely to receive the programme. I can therefore compare regions on either side of the literacy-rate cut-off to determine the causal impact of the policy. The RD design allows me to tackle biases that may arise when estimating the individual returns to education, and when comparing earnings in two different local economies.

To support each piece of the general equilibrium model, I create a comprehensive dataset and then use the data to estimate the returns to education and the GE effects. I do this by exploiting not just the RD, but also the variation in cohort exposure and skill levels. Younger cohorts can change their educational attainment in response to the policy, whereas older cohorts cannot. Both the young and the old are, however, affected by changes in the labour market skill distribution and the movement of firms. Furthermore, since the young and the old are not perfect substitutes in the labour market, the GE effects on the two cohorts must be estimated separately. The change in the earnings skill-premium (which help determine the returns to more years of education) for older workers tells me the part of the GE effects that affect all cohorts, whereas the change in skill-premium for younger workers helps me derive the additional impact on younger workers.

Figure 1: Allocation rule of District Primary Education Programme (DPEP)

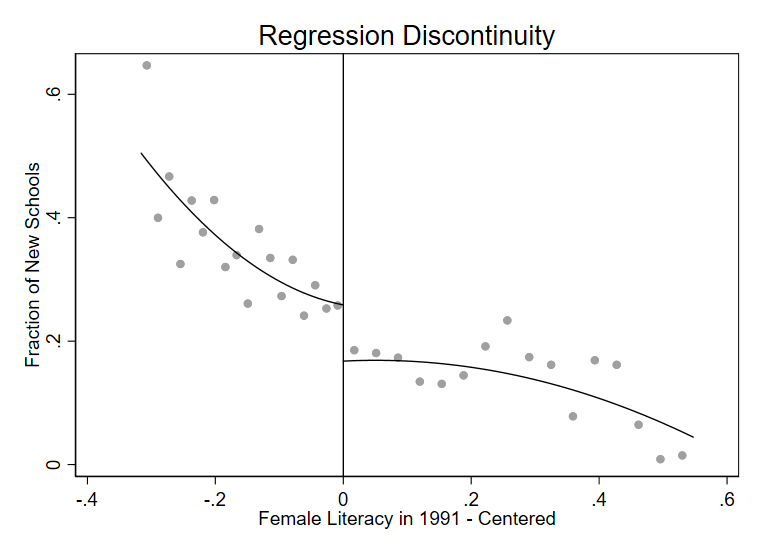
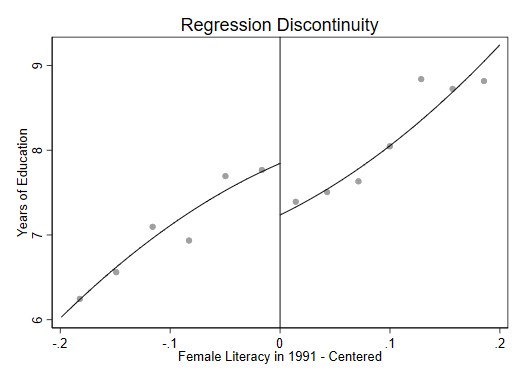
Impacts of this programme for students

I find that the programme increased both education and earnings for students in targeted regions. In the figure alongside, I show that at the RD cut-off there were more new schools and young workers had more education. Overall welfare increases are driven by reductions in the costs of education and an increase in the overall output of the region. However, general equilibrium effects substantially mitigate the rise in labour market welfare. 

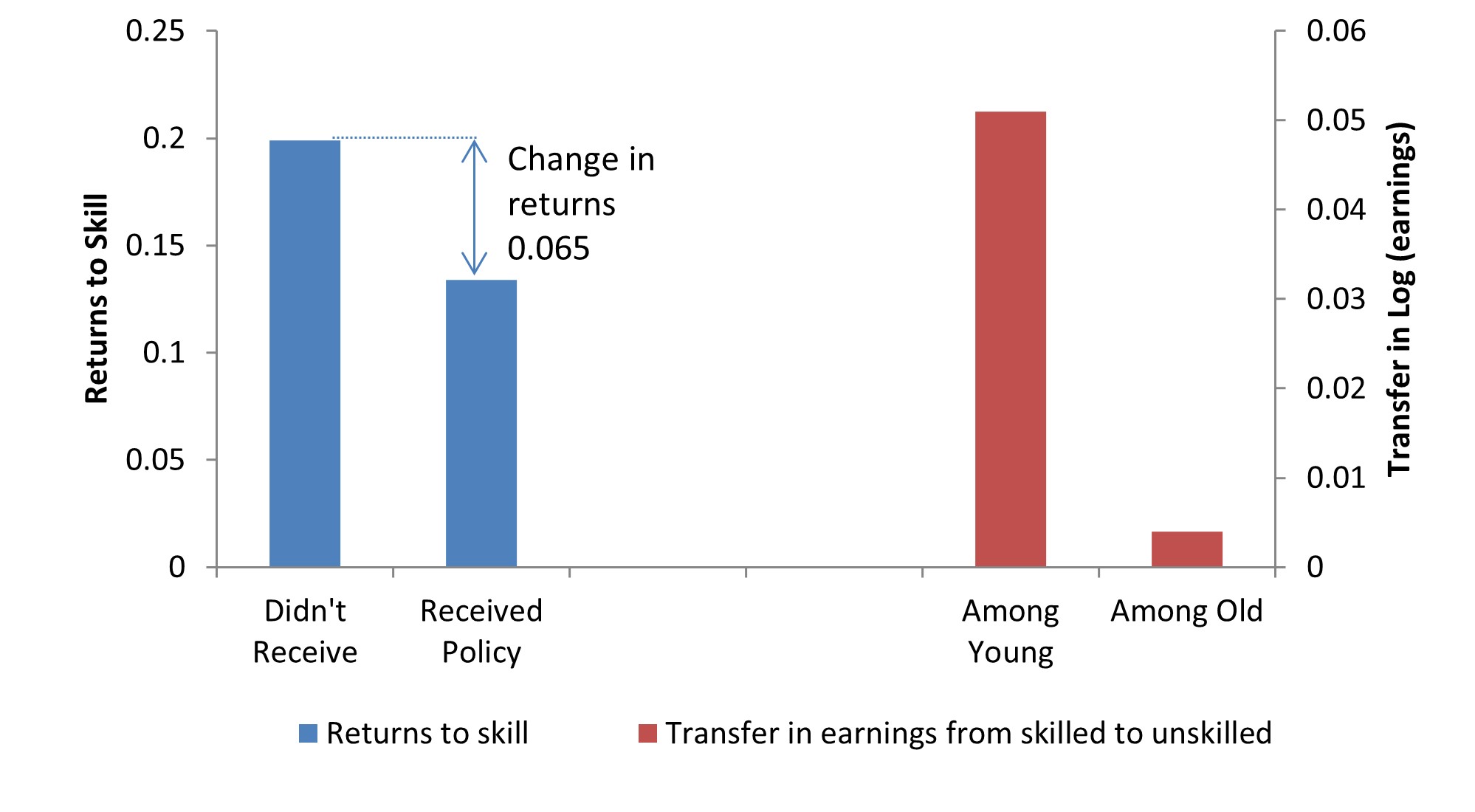
Increases in the supply of educated workers dampened earnings for skilled workers and put upward pressure on the earnings of unskilled workers. The returns to skill are 13.4%, but the estimated labour market GE effects are substantial – they depress the returns by 6.5 percentage points – down from 19.9% – and dampen the increase in student welfare by 23%. These GE effects have important distributional consequences, with a transfer of labour-market benefits from skilled to unskilled workers, particularly among the younger cohorts. High-skill workers who did not change their educational levels under the policy are adversely affected in the labour market, whereas low-skill workers benefit.

Figure 2: Returns to skill accounting for economy wide changes

Taking stock: Putting these effects into context

One crucial concern with an expansion in public schooling is that it may crowd out private supply. On the other hand, a crowd-in could also have occurred if the programme increased the overall size and demand for a skilled workforce. Understanding how private schools respond is, therefore, essential to identifying the overall welfare benefits, as a large amount of crowd-out implies that the funds are essentially wasted and could have been spent on other programmes. In my context, I find an influx of private schools when public schooling is expanded.

The results in this paper indicate that these wage responses may undermine some of the effectiveness of micro-interventions when they are scaled up. On the other hand, the crowd-in of private schools indicate that large-scale public schooling expansions may have other unintended benefits in the education sector. I also show that once the funding was phased out, certain crucial inputs, like college-educated teachers no longer remain. These empirically important consequences are crucial considerations for both researchers and policy-makers who examine or implement such large-scale interventions.

References

Card, D, and T Lemieux (2001), “Can Falling Supply Explain the Rising Return to College for Younger Men? A Cohort-Based Analysis.” The Quarterly Journal of Economics, 116(2): 705–46.

Heckman, J J & L Lochner, and C Taber (1998), "General-Equilibrium Treatment Effects: A Study of Tuition Policy," American Economic Review, 88(2): 381-386.

Khanna, G (2023), “Large-Scale Education Reform in General Equilibrium: Regression Discontinuity Evidence from India.” Journal of Political Economy.

Mincer, J (1975), “Education, Experience, and the Distribution of Earnings and Employment: An Overview.” Education, Income, and Human Behavior (F. Thomas Juster, ed.) NBER

Muralidharan, K, A Singh, and A J Ganimian (2019), "Disrupting Education? Experimental Evidence on Technology-Aided Instruction in India." American Economic Review, 109(4): 1426-60.